线性代数笔记(二)
2. 更多向量的高级话题
2.1. 规范化和单位向量
- 向量的长度
- 作为有向线段,向量既有方向也有大小
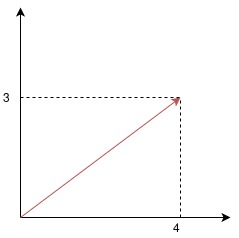
根据勾股定理有:
\[\vec{u}\text{的长度} = \sqrt{3^2+4^2} = 5\]记作:
\[||\vec{u}|| = \sqrt{3^2+4^2} = 5\]其中:
\[||\vec{u}||\text{,或可记作:}|\vec{u}|\]即为向量的模
-
三维空间内向量的模:
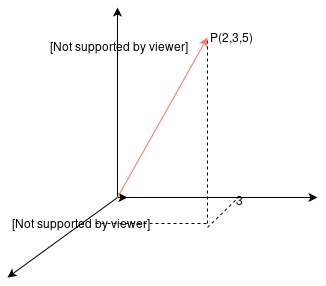
如图:
\[\vec{u} = \overrightarrow{OP} = (2,3,5)\]则:
\[\vec{u} = \sqrt{2^2+3^2+5^2}\] -
n维向量同理:
\[\vec{u} = (u_1,u_2,\dots,u_n)^{T}\\[7pt] |\vec{u}| = \sqrt{u_1^2+u_2^2+...+u_n^2}\] - 单位向量:
-
根据$\vec{u}$求出$\hat{u}$的过程:归一化,规范化(normalize)
-
单位向量有无数个:
- 单位圆内从原点到圆上任何一点
-
二维空间中,有两个特殊的单位向量:
\[\vec{e_1} = (1,0)\qquad\vec{e_2} = (0,1)\]只有0,1组成的单位向量:标准单位向量(Standard Unit Vector) 它们指向坐标轴的正方向
- 二维空间中有两个标准单位向量
- 三维空间中有三个
- n为空间中有n个标准单位向量
2.2. 实现向量规范化和单位向量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import math
from ._global import EPSILON
class vector:
def __init__(self,lst):
self._values = list(lst)
#构造函数,初始化类,将数组传入,用list方法复制lst变量,确保vector不可更改性
@classmethod
def zero(cls,dim):
#返回一个dim维的零向量
return cls([0]*dim)
def norm(self):
return math.sqrt(sum(e**2 for e in self))
#求模运算
def normalize(self):
#求单位向量,即规范化
return Vector([e/ self.norm() for e in self])
#also write as : return 1/ self.norm()*Vcctor(self._values)
def __truediv__(self,k):
#向量数量除法
if self.norm <EPSILON :
raise "Error"
#为了甄别零向量,需要加一个前提判断,
#即模如果为零,则范围Error,
#但浮点数判断不可用‘==’,故而需要使用极限法,
#定义一个全局私有变量`EPSILON`,
#在包内增加一个`_global.py`文件
return (1/k)*self
_global.py文件:
1
EPSILON = 1e-8
2.3. 向量的点乘
- 两个向量相乘
两个向量“相乘”,结果是一个数(标量) 更严格的说法:两个向量的点乘(内积)
\[\vec{u}·\vec{v} = |\vec{u}|·|\vec{v}|·\cos{\theta}\]- 证明:
如图,
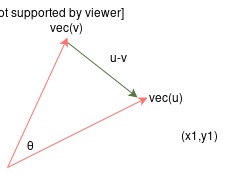
二维空间中:
\[\vec{u}·\vec{v} = x_1·x_2+y_1·y_2 = |\vec{u}|·|\vec{v}|·\cos{\theta}\\[7pt]\]由三角形,有:
\[|\vec{u} - \vec{v}|^2 = |\vec{u}|^2+|\vec{v}|^2-2· |\vec{u}|^2·|\vec{v}|^2·\cos{\theta}\]移项,得:
\[2· |\vec{u}|^2·|\vec{v}|^2·\cos{\theta} = |\vec{u}|^2+|\vec{v}|^2-|\vec{u} - \vec{v}|^2\]两边除以$\frac{1}{2}$,得:
\[|\vec{u}|^2·|\vec{v}|^2·\cos{\theta} = \frac{1}{2}(|\vec{u}|^2+|\vec{v}|^2-|\vec{u} - \vec{v}|^2)\]展开整理,得:
\[\frac{1}{2}(|\vec{u}|^2+|\vec{v}|^2-|\vec{u} - \vec{v}|^2) = \frac{1}{2}((x_1+y_1)^2+(x_2+y_2)^2-(x_1-x_2)^2-(y_1-y_2)^2)\\[10pt] \frac{1}{2}(|\vec{u}|^2+|\vec{v}|^2-|\vec{u} - \vec{v}|^2) =\frac{1}{2}(x_1^2+y_1^2+x_2^2+y_2^2-x_1^2-x_2^2+2x_1x_2-y_1^2-y_2^2+2y_1y_2)\\[10pt] \frac{1}{2}(|\vec{u}|^2+|\vec{v}|^2-|\vec{u} - \vec{v}|^2) = x_1x_2+y_1y_2 = \vec{u}·\vec{v}\\[10pt] \text{Q.E.D.}\]同理,n维向量有:
\[\vec{u}·\vec{v} = u_1·v_1+\dots+u_n·v_n = |\vec{u}|·|\vec{v}|·\cos{\theta}\]2.4. 向量点乘的几何理解
如图:
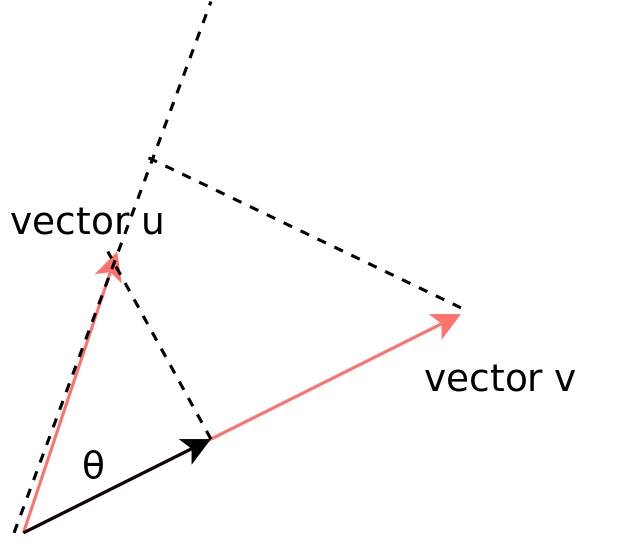
可以看到,$\text{向量同}\cos{\theta}\text{相乘}$实际上就是将原向量投影到另外一个向量的同一方向
2.5. 实现向量点乘
1
2
3
4
#单独设立一个方法`dot`来标记向量点乘
def dot(self,another):
assert len(self) == len(another),"Error"
return sum(a*b for a,b in zip(self,another))
- 有些数学库会将u*v定义为逐元素相乘的向量,由于这个计算不具备数学含义,所以实现中不取
2.6. 向量点乘的意义
- 向量点乘的应用:
可得:
\[\cos{\theta} = \frac{\vec{u}·\vec{v}}{|\vec{u}|·|\vec{v}|},\text{特别的,如果}\theta = \frac{\pi}{4},\vec{u}·\vec{v} = 0\\[10pt] \text{如果}\vec{u}·\vec{v} = 0,\text{两个向量垂直};\\[10pt] \text{如果}\vec{u}·\vec{v} > 0,\text{两个向量夹角为锐角};\\[10pt] \text{如果}\vec{u}·\vec{v} < 0,\text{两个向量夹角为钝角}\]回忆标准单位向量
二维空间:
\[\vec{e_1} = (1,0)\qquad\vec{e_2} = (0,1)\qquad\vec{e_1}·\vec{e_2} = 0\]三维空间:
\[\vec{e_1} = (1,0,0)\qquad\vec{e_2} = (0,1,0)\qquad\vec{e_3} = (0,0,1)\\[10pt] \vec{e_1}·\vec{e_2} =0\qquad\vec{e_1}·\vec{e_3} = 0\qquad\vec{e_2} ·\vec{e_3} =0\]判断两个向量的相似程度(推荐系统)
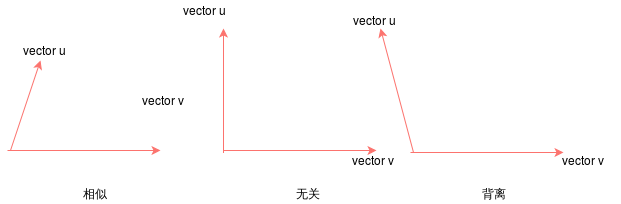
几何计算
- 求取向量投影点的点坐标
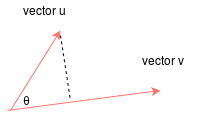
投影点的距离:
\[d = |\vec{v}|\cos{\theta} = \frac{\vec{u}·\vec{v}}{|\vec{u}|}\]投影点的方向(单位向量):$\hat{u}$
投影点的坐标:
\[P_v = d·\hat{u}\]2.7. Numpy的使用
1
2
3
4
5
6
7
import numpy as np
if __name__ == "__main__":
print(np.__version__)
vec = np.array([1,2.3])
#np数组存储向量

